AES: Difference between revisions
No edit summary |
|||
| (14 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
Strictly speaking, AES is not precisely Rijndael (although in practice they are used interchangeably) as Rijndael supports a larger range of [[block size (cryptography)|block]] and [[key size]]s; AES has a fixed block size of 128 bits and a key size of 128, 192, or 256 bits, whereas Rijndael can be specified with key and block sizes in any multiple of 32 bits, with a minimum of 128 bits and a maximum of 256 bits. | Strictly speaking, AES is not precisely Rijndael (although in practice they are used interchangeably) as Rijndael supports a larger range of [[block size (cryptography)|block]] and [[key size]]s; AES has a fixed block size of 128 bits and a key size of 128, 192, or 256 bits, whereas Rijndael can be specified with key and block sizes in any multiple of 32 bits, with a minimum of 128 bits and a maximum of 256 bits. | ||
Due to the fixed block size of 128 bits, AES operates on a 4×4 array of bytes, termed the ''state'' (versions of Rijndael with a larger block size have additional columns in the state). Most AES calculations are done in a special finite field. | Due to the fixed block size of 128 bits, AES operates on a 4×4 array of bytes, termed the ''state'' (versions of Rijndael with a larger block size have additional columns in the state). Most AES calculations are done in a special finite field.<br> | ||
<br> | |||
=== High-level cipher algorithm === | === High-level cipher algorithm === | ||
* KeyExpansion using [[Rijndael key schedule|Rijndael's key schedule]] | * KeyExpansion using [[Rijndael key schedule|Rijndael's key schedule]] | ||
* Initial Round | * Initial Round | ||
| Line 23: | Line 23: | ||
# <tt>SubBytes</tt> | # <tt>SubBytes</tt> | ||
# <tt>ShiftRows</tt> | # <tt>ShiftRows</tt> | ||
# <tt>AddRoundKey</tt> | # <tt>AddRoundKey</tt><br> | ||
<br> | |||
===The <tt>SubBytes</tt> step=== | ===The <tt>SubBytes</tt> step=== | ||
[[Image:AES-SubBytes.png|right|320px|thumbnail|In the <tt>SubBytes</tt> step, each byte in the state is replaced with its entry in a fixed 8-bit lookup table, ''S''; ''b<sub>ij</sub>'' = ''S(a<sub>ij</sub>)''.]] | [[Image:AES-SubBytes.png|right|320px|thumbnail|In the <tt>SubBytes</tt> step, each byte in the state is replaced with its entry in a fixed 8-bit lookup table, ''S''; ''b<sub>ij</sub>'' = ''S(a<sub>ij</sub>)''.]] | ||
In the <tt>SubBytes</tt> step, each byte in the array is updated using an 8-bit [[substitution box]], the [[Rijndael S-box]]. This operation provides the non-linearity in the [[cipher]]. The S-box used is derived from the [[multiplicative inverse]] over '''[[Finite field|GF]]'''(''2<sup>8</sup>''), known to have good non-linearity properties. To avoid attacks based on simple algebraic properties, the S-box is constructed by combining the inverse function with an invertible [[affine transformation]]. The S-box is also chosen to avoid any fixed points (and so is a [[derangement]]), and also any opposite fixed points. | In the <tt>SubBytes</tt> step, each byte in the array is updated using an 8-bit [[substitution box]], the [[Rijndael S-box]]. This operation provides the non-linearity in the [[cipher]]. The S-box used is derived from the [[multiplicative inverse]] over '''[[Finite field|GF]]'''(''2<sup>8</sup>''), known to have good non-linearity properties. To avoid attacks based on simple algebraic properties, the S-box is constructed by combining the inverse function with an invertible [[affine transformation]]. The S-box is also chosen to avoid any fixed points (and so is a [[derangement]]), and also any opposite fixed points.<br> | ||
<br> | |||
===The <tt>ShiftRows</tt> step=== | ===The <tt>ShiftRows</tt> step=== | ||
[[Image:AES-ShiftRows.png|right|320px|thumbnail|In the <tt>ShiftRows</tt> step, bytes in each row of the state are shifted cyclically to the left. The number of places each byte is shifted differs for each row.]] | [[Image:AES-ShiftRows.png|right|320px|thumbnail|In the <tt>ShiftRows</tt> step, bytes in each row of the state are shifted cyclically to the left. The number of places each byte is shifted differs for each row.]] | ||
The <tt>ShiftRows</tt> step operates on the rows of the state; it cyclically shifts the bytes in each row by a certain [[Offset (computer science)|offset]]. For AES, the first row is left unchanged. Each byte of the second row is shifted one to the left. Similarly, the third and fourth rows are shifted by offsets of two and three respectively. For the block of size 128 bits and 192 bits the shifting pattern is the same. In this way, each column of the output state of the <tt>ShiftRows</tt> step is composed of bytes from each column of the input state. (Rijndael variants with a larger block size have slightly different offsets). In the case of the 256-bit block, the first row is unchanged and the shifting for second, third and fourth row is 1 byte, 3 byte and 4 byte respectively - although this change only applies for the Rijndael cipher when used with a 256-bit block, which is not used for AES. | The <tt>ShiftRows</tt> step operates on the rows of the state; it cyclically shifts the bytes in each row by a certain [[Offset (computer science)|offset]]. For AES, the first row is left unchanged. Each byte of the second row is shifted one to the left. Similarly, the third and fourth rows are shifted by offsets of two and three respectively. For the block of size 128 bits and 192 bits the shifting pattern is the same. In this way, each column of the output state of the <tt>ShiftRows</tt> step is composed of bytes from each column of the input state. (Rijndael variants with a larger block size have slightly different offsets). In the case of the 256-bit block, the first row is unchanged and the shifting for second, third and fourth row is 1 byte, 3 byte and 4 byte respectively - although this change only applies for the Rijndael cipher when used with a 256-bit block, which is not used for AES.<br> | ||
<br> | |||
===The <tt>MixColumns</tt> step=== | ===The <tt>MixColumns</tt> step=== | ||
[[Image:AES-MixColumns.png|right|320px|thumbnail|In the <tt>MixColumns</tt> step, each column of the state is multiplied with a fixed polynomial ''c(x)''.]] | [[Image:AES-MixColumns.png|right|320px|thumbnail|In the <tt>MixColumns</tt> step, each column of the state is multiplied with a fixed polynomial ''c(x)''.]] | ||
In the <tt>MixColumns</tt> step, the four bytes of each column of the state are combined using an invertible [[linear transformation]]. The <tt>MixColumns</tt> function takes four bytes as input and outputs four bytes, where each input byte affects all four output bytes. Together with <tt>ShiftRows</tt>, <tt>MixColumns</tt> provides [[diffusion (cryptography)|diffusion]] in the cipher. Each column is treated as a polynomial over '''GF'''(''2<sup>8</sup>'') and is then multiplied modulo with a fixed polynomial. The <tt>MixColumns</tt> step can also be viewed as a multiplication by a particular MDS matrix in Finite field arithmetic. | In the <tt>MixColumns</tt> step, the four bytes of each column of the state are combined using an invertible [[linear transformation]]. The <tt>MixColumns</tt> function takes four bytes as input and outputs four bytes, where each input byte affects all four output bytes. Together with <tt>ShiftRows</tt>, <tt>MixColumns</tt> provides [[diffusion (cryptography)|diffusion]] in the cipher. Each column is treated as a polynomial over '''GF'''(''2<sup>8</sup>'') and is then multiplied modulo with a fixed polynomial. The <tt>MixColumns</tt> step can also be viewed as a multiplication by a particular MDS matrix in Finite field arithmetic.<br> | ||
<br> | |||
===The <tt>AddRoundKey</tt> step=== | ===The <tt>AddRoundKey</tt> step=== | ||
[[Image:AES-AddRoundKey.png|right|320px|thumbnail|In the <tt>AddRoundKey</tt> step, each byte of the state is combined with a byte of the round subkey using the [[Exclusive or|XOR]] operation (⊕).]] | [[Image:AES-AddRoundKey.png|right|320px|thumbnail|In the <tt>AddRoundKey</tt> step, each byte of the state is combined with a byte of the round subkey using the [[Exclusive or|XOR]] operation (⊕).]] | ||
In the <tt>AddRoundKey</tt> step, the subkey is combined with the state. For each round, a subkey is derived from the main [[key (cryptography)|key]] using [[Rijndael key schedule|Rijndael's key schedule]]; each subkey is the same size as the state. The subkey is added by combining each byte of the state with the corresponding byte of the subkey using bitwise [[Exclusive or|XOR]]. | In the <tt>AddRoundKey</tt> step, the subkey is combined with the state. For each round, a subkey is derived from the main [[key (cryptography)|key]] using [[Rijndael key schedule|Rijndael's key schedule]]; each subkey is the same size as the state. The subkey is added by combining each byte of the state with the corresponding byte of the subkey using bitwise [[Exclusive or|XOR]].<br> | ||
<br> | |||
===Optimization of the cipher=== | ===Optimization of the cipher=== | ||
| Line 46: | Line 51: | ||
If the resulting four kilobyte table size is too large for a given target platform, the table lookup operation can be performed with a single 256-entry 32-bit table by the use of circular rotates. | If the resulting four kilobyte table size is too large for a given target platform, the table lookup operation can be performed with a single 256-entry 32-bit table by the use of circular rotates. | ||
Using a byte-oriented approach it is possible to combine the <tt>SubBytes</tt>, <tt>ShiftRows</tt>, and <tt>MixColumns</tt> steps into a single round operation. | Using a byte-oriented approach it is possible to combine the <tt>SubBytes</tt>, <tt>ShiftRows</tt>, and <tt>MixColumns</tt> steps into a single round operation.<br> | ||
<br> | |||
==Security== | ==Security== | ||
As of 2006, the only successful attacks against AES implementations have been [[side channel attack]]s. The | As of 2006, the only successful attacks against AES implementations have been [[side channel attack]]s. The National Security Agency (NSA) reviewed all the AES finalists, including Rijndael, and stated that all of them were secure enough for US Government non-classified data. In June 2003, the US Government announced that AES may be used for [[classified information]]: | ||
:"''The design and strength of all key lengths of the AES algorithm (i.e., 128, 192 and 256) are sufficient to protect classified information up to the SECRET level. TOP SECRET information will require use of either the 192 or 256 key lengths. The implementation of AES in products intended to protect national security systems and/or information must be reviewed and certified by NSA prior to their acquisition and use. | :"''The design and strength of all key lengths of the AES algorithm (i.e., 128, 192 and 256) are sufficient to protect classified information up to the SECRET level. TOP SECRET information will require use of either the 192 or 256 key lengths. The implementation of AES in products intended to protect national security systems and/or information must be reviewed and certified by NSA prior to their acquisition and use. This marks the first time that the public has had access to a cipher approved by NSA for encryption of TOP SECRET information. Many public products use 128-bit secret keys by default; it is possible that NSA suspects a fundamental weakness in keys this short, or they may simply prefer a safety margin for top secret documents (which may require security decades into the future). | ||
This marks the first time that the public has had access to a cipher approved by NSA for encryption of TOP SECRET information. Many public products use 128-bit secret keys by default; it is possible that NSA suspects a fundamental weakness in keys this short, or they may simply prefer a safety margin for top secret documents (which may require security decades into the future). | |||
The most common way to attack block ciphers is to try various attacks on versions of the cipher with a reduced number of rounds. AES has 10 rounds for 128-bit keys, 12 rounds for 192-bit keys, and 14 rounds for 256-bit keys. By 2006, the best known attacks were on 7 rounds for 128-bit keys, 8 rounds for 192-bit keys, and 9 rounds for 256-bit keys. | The most common way to attack block ciphers is to try various attacks on versions of the cipher with a reduced number of rounds. AES has 10 rounds for 128-bit keys, 12 rounds for 192-bit keys, and 14 rounds for 256-bit keys. By 2006, the best known attacks were on 7 rounds for 128-bit keys, 8 rounds for 192-bit keys, and 9 rounds for 256-bit keys. | ||
Some cryptographers worry about the security of AES. They feel that the margin between the number of rounds specified in the cipher and the best known attacks is too small for comfort. There is a risk that some way to improve such attacks might be found and then the cipher could be broken. In this meaning, a [[cryptanalysis|cryptographic]] "break" is anything faster than an [[brute force attack|exhaustive search]], thus an attack against a 128-bit-key AES requiring 'only' 2<sup>120</sup> operations (compared to 2<sup>128</sup> possible keys) would be considered a break even though it would be, at present, quite infeasible. In practical application, any break of AES which is only that "good" would be irrelevant. At present, such concerns can be ignored. The largest successful publicly-known [[brute force attack]] has been against a 64-bit [[RC5]] key by [[distributed.net]]. | Some cryptographers worry about the security of AES. They feel that the margin between the number of rounds specified in the cipher and the best known attacks is too small for comfort. There is a risk that some way to improve such attacks might be found and then the cipher could be broken. In this meaning, a [[cryptanalysis|cryptographic]] "break" is anything faster than an [[brute force attack|exhaustive search]], thus an attack against a 128-bit-key AES requiring 'only' 2<sup>120</sup> operations (compared to 2<sup>128</sup> possible keys) would be considered a break even though it would be, at present, quite infeasible. In practical application, any break of AES which is only that "good" would be irrelevant. At present, such concerns can be ignored. The largest successful publicly-known [[brute force attack]] has been against a 64-bit [[RC5]] key by [[distributed.net]]. | ||
Other debates centers around the | Other debates centers around the mathematical structure of AES. Unlike most other block ciphers, AES has a very neat algebraic description. This has not yet led to any attacks, but some researchers feel that basing a cipher on a new hardness assumption is risky. This has led Ferguson, Schroeppel, and Whiting to write, "...we are concerned about the use of Rijndael [AES] in security-critical applications. | ||
In | In 2002, a theoretical attack, termed the "[[XSL attack]]", was announced by Nicolas Courtois and Josef Pieprzyk, showing a potential weakness in the AES algorithm. Several cryptography experts have found problems in the underlying mathematics of the proposed attack, suggesting that the authors may have made a mistake in their estimates. Whether this line of attack can be made to work against AES remains an open question. At present, the XSL attack against AES appears speculative; it is unlikely that the current attack could be carried out in practice. | ||
===Side channel attacks=== | ===Side channel attacks=== | ||
[[Side channel attack]]s do not attack the underlying cipher and so have nothing to do with its security as described here, but attack implementations of the cipher on systems which inadvertently leak data. There are several such known attacks on certain implementations of AES. | [[Side channel attack]]s do not attack the underlying cipher and so have nothing to do with its security as described here, but attack implementations of the cipher on systems which inadvertently leak data. There are several such known attacks on certain implementations of AES. | ||
In April 2005, | In April 2005, Daniel J. Bernstein announced a cache timing attack that he used to break a custom server that used [[OpenSSL]]'s AES encryption. The custom server was designed to give out as much timing information as possible, and the attack required over 200 million chosen plaintexts. Some say the attack is not practical over the internet with a distance of one or more hops. | ||
In October 2005, Dag Arne Osvik, | In October 2005, Dag Arne Osvik, Adi Shamir and Eran Tromer presented a paper demonstrating several cache timing attacks against AES. One attack was able to obtain an entire AES key after only 800 operations triggering encryptions, in a total of 65 milliseconds. This attack requires the attacker to be able to run programs on the same system that is performing AES.<br> | ||
<br> | |||
==FIPS Validation== | ==FIPS Validation== | ||
The Cryptographic Module Validation Program (CMVP) is operated jointly by the United States Government's National Institute of Standards and Technology (NIST) Computer Security Division and the Communications Security Establishment (CSE) of the Government of Canada. The use of validated cryptographic modules is required by the United States Government for all unclassified uses of cryptography. The Government of Canada also recommends the use of [[FIPS 140]] validated cryptographic modules in unclassified applications of its departments. | |||
The | |||
Although NIST publication 197 ("FIPS 197") is the unique document that covers the AES algorithm, vendors typically approach the CMVP under FIPS 140 and ask to have several algorithms (such as [[3DES]] or [[SHA1]]) validated at the same time. Therefore, it is rare to find cryptographic modules that are uniquely FIPS 197 validated and NIST itself does not generally take the time to list FIPS 197 validated modules separately on its public web site. Instead, FIPS 197 validation is typically just listed as an "FIPS approved: AES" notation (with a specific FIPS 197 certificate number) in the current list of FIPS 140 validated cryptographic modules. | Although NIST publication 197 ("FIPS 197") is the unique document that covers the AES algorithm, vendors typically approach the CMVP under FIPS 140 and ask to have several algorithms (such as [[3DES]] or [[SHA1]]) validated at the same time. Therefore, it is rare to find cryptographic modules that are uniquely FIPS 197 validated and NIST itself does not generally take the time to list FIPS 197 validated modules separately on its public web site. Instead, FIPS 197 validation is typically just listed as an "FIPS approved: AES" notation (with a specific FIPS 197 certificate number) in the current list of FIPS 140 validated cryptographic modules. | ||
FIPS validation is challenging to achieve both technically and fiscally. There is a standardized battery of tests as well as an element of source code review that must be passed over a period of several days. The cost to perform these tests through an approved laboratory can be significant (e.g., well over $10,000 US) and does not include the time it takes to write, test, document and prepare a module for validation. After validation, modules must be resubmitted and reevaluated if they are changed in any way. | FIPS validation is challenging to achieve both technically and fiscally. There is a standardized battery of tests as well as an element of source code review that must be passed over a period of several days. The cost to perform these tests through an approved laboratory can be significant (e.g., well over $10,000 US) and does not include the time it takes to write, test, document and prepare a module for validation. After validation, modules must be resubmitted and reevaluated if they are changed in any way.<br> | ||
<br> | |||
==See also== | ==See also== | ||
Latest revision as of 11:41, 28 March 2008
In cryptography, the Advanced Encryption Standard (AES), also known as Rijndael, is a block cipher adopted as an encryption standard by the Federal government of the United States. It has been analyzed extensively and is now used worldwide, as was the case with its predecessor, the Data Encryption Standard (DES). AES was announced by National Institute of Standards and Technology (NIST) as U.S. FIPS PUB 197 (FIPS 197) on November 26 2001 after a 5-year standardization process. It became effective as a standard May 26, 2002. As of 2006, AES is one of the most popular algorithms used in symmetric key cryptography. It is available by choice in many different encryption packages.
The cipher was developed by two Belgian cryptographers, Joan Daemen and Vincent Rijmen, and submitted to the AES selection process under the name "Rijndael", a portmanteau of the names of the inventors.
Unlike DES, its predecessor, Rijndael is a substitution-permutation network, not a Feistel network. AES is fast in both computer software and hardware, is relatively easy to implement, and requires little computer memory. As a new encryption standard, it is currently being deployed on a large scale.
Description of the cipher
Strictly speaking, AES is not precisely Rijndael (although in practice they are used interchangeably) as Rijndael supports a larger range of block and key sizes; AES has a fixed block size of 128 bits and a key size of 128, 192, or 256 bits, whereas Rijndael can be specified with key and block sizes in any multiple of 32 bits, with a minimum of 128 bits and a maximum of 256 bits.
Due to the fixed block size of 128 bits, AES operates on a 4×4 array of bytes, termed the state (versions of Rijndael with a larger block size have additional columns in the state). Most AES calculations are done in a special finite field.
High-level cipher algorithm
- KeyExpansion using Rijndael's key schedule
- Initial Round
- AddRoundKey
- Rounds
- SubBytes — a non-linear substitution step where each byte is replaced with another according to a lookup table.
- ShiftRows — a transposition step where each row of the state is shifted cyclically a certain number of steps.
- MixColumns — a mixing operation which operates on the columns of the state, combining the four bytes in each column
- AddRoundKey — each byte of the state is combined with the round key; each round key is derived from the cipher key using a key schedule.
- Final Round (no MixColumns)
- SubBytes
- ShiftRows
- AddRoundKey
The SubBytes step
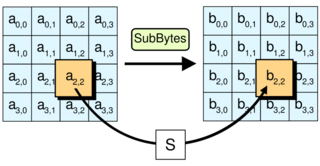
In the SubBytes step, each byte in the array is updated using an 8-bit substitution box, the Rijndael S-box. This operation provides the non-linearity in the cipher. The S-box used is derived from the multiplicative inverse over GF(28), known to have good non-linearity properties. To avoid attacks based on simple algebraic properties, the S-box is constructed by combining the inverse function with an invertible affine transformation. The S-box is also chosen to avoid any fixed points (and so is a derangement), and also any opposite fixed points.
The ShiftRows step
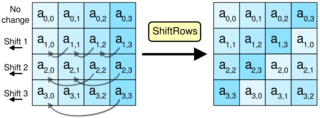
The ShiftRows step operates on the rows of the state; it cyclically shifts the bytes in each row by a certain offset. For AES, the first row is left unchanged. Each byte of the second row is shifted one to the left. Similarly, the third and fourth rows are shifted by offsets of two and three respectively. For the block of size 128 bits and 192 bits the shifting pattern is the same. In this way, each column of the output state of the ShiftRows step is composed of bytes from each column of the input state. (Rijndael variants with a larger block size have slightly different offsets). In the case of the 256-bit block, the first row is unchanged and the shifting for second, third and fourth row is 1 byte, 3 byte and 4 byte respectively - although this change only applies for the Rijndael cipher when used with a 256-bit block, which is not used for AES.
The MixColumns step
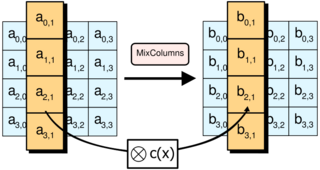
In the MixColumns step, the four bytes of each column of the state are combined using an invertible linear transformation. The MixColumns function takes four bytes as input and outputs four bytes, where each input byte affects all four output bytes. Together with ShiftRows, MixColumns provides diffusion in the cipher. Each column is treated as a polynomial over GF(28) and is then multiplied modulo with a fixed polynomial. The MixColumns step can also be viewed as a multiplication by a particular MDS matrix in Finite field arithmetic.
The AddRoundKey step
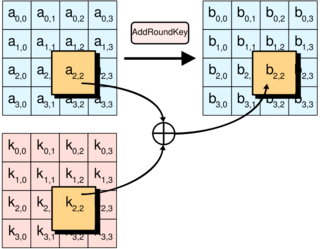
In the AddRoundKey step, the subkey is combined with the state. For each round, a subkey is derived from the main key using Rijndael's key schedule; each subkey is the same size as the state. The subkey is added by combining each byte of the state with the corresponding byte of the subkey using bitwise XOR.
Optimization of the cipher
On systems with 32-bit or larger words, it is possible to speed up execution of this cipher by combining SubBytes and ShiftRows with MixColumns, and transforming them into a sequence of table lookups. This requires four 256-entry 32-bit tables, which utilizes a total of four kilobytes (4096 bytes) of memory--one kilobyte for each table. A round can now be done with 16 table lookups and 12 32-bit exclusive-or operations, followed by four 32-bit exclusive-or operations in the AddRoundKey step.
If the resulting four kilobyte table size is too large for a given target platform, the table lookup operation can be performed with a single 256-entry 32-bit table by the use of circular rotates.
Using a byte-oriented approach it is possible to combine the SubBytes, ShiftRows, and MixColumns steps into a single round operation.
Security
As of 2006, the only successful attacks against AES implementations have been side channel attacks. The National Security Agency (NSA) reviewed all the AES finalists, including Rijndael, and stated that all of them were secure enough for US Government non-classified data. In June 2003, the US Government announced that AES may be used for classified information:
- "The design and strength of all key lengths of the AES algorithm (i.e., 128, 192 and 256) are sufficient to protect classified information up to the SECRET level. TOP SECRET information will require use of either the 192 or 256 key lengths. The implementation of AES in products intended to protect national security systems and/or information must be reviewed and certified by NSA prior to their acquisition and use. This marks the first time that the public has had access to a cipher approved by NSA for encryption of TOP SECRET information. Many public products use 128-bit secret keys by default; it is possible that NSA suspects a fundamental weakness in keys this short, or they may simply prefer a safety margin for top secret documents (which may require security decades into the future).
The most common way to attack block ciphers is to try various attacks on versions of the cipher with a reduced number of rounds. AES has 10 rounds for 128-bit keys, 12 rounds for 192-bit keys, and 14 rounds for 256-bit keys. By 2006, the best known attacks were on 7 rounds for 128-bit keys, 8 rounds for 192-bit keys, and 9 rounds for 256-bit keys.
Some cryptographers worry about the security of AES. They feel that the margin between the number of rounds specified in the cipher and the best known attacks is too small for comfort. There is a risk that some way to improve such attacks might be found and then the cipher could be broken. In this meaning, a cryptographic "break" is anything faster than an exhaustive search, thus an attack against a 128-bit-key AES requiring 'only' 2120 operations (compared to 2128 possible keys) would be considered a break even though it would be, at present, quite infeasible. In practical application, any break of AES which is only that "good" would be irrelevant. At present, such concerns can be ignored. The largest successful publicly-known brute force attack has been against a 64-bit RC5 key by distributed.net.
Other debates centers around the mathematical structure of AES. Unlike most other block ciphers, AES has a very neat algebraic description. This has not yet led to any attacks, but some researchers feel that basing a cipher on a new hardness assumption is risky. This has led Ferguson, Schroeppel, and Whiting to write, "...we are concerned about the use of Rijndael [AES] in security-critical applications.
In 2002, a theoretical attack, termed the "XSL attack", was announced by Nicolas Courtois and Josef Pieprzyk, showing a potential weakness in the AES algorithm. Several cryptography experts have found problems in the underlying mathematics of the proposed attack, suggesting that the authors may have made a mistake in their estimates. Whether this line of attack can be made to work against AES remains an open question. At present, the XSL attack against AES appears speculative; it is unlikely that the current attack could be carried out in practice.
Side channel attacks
Side channel attacks do not attack the underlying cipher and so have nothing to do with its security as described here, but attack implementations of the cipher on systems which inadvertently leak data. There are several such known attacks on certain implementations of AES.
In April 2005, Daniel J. Bernstein announced a cache timing attack that he used to break a custom server that used OpenSSL's AES encryption. The custom server was designed to give out as much timing information as possible, and the attack required over 200 million chosen plaintexts. Some say the attack is not practical over the internet with a distance of one or more hops.
In October 2005, Dag Arne Osvik, Adi Shamir and Eran Tromer presented a paper demonstrating several cache timing attacks against AES. One attack was able to obtain an entire AES key after only 800 operations triggering encryptions, in a total of 65 milliseconds. This attack requires the attacker to be able to run programs on the same system that is performing AES.
FIPS Validation
The Cryptographic Module Validation Program (CMVP) is operated jointly by the United States Government's National Institute of Standards and Technology (NIST) Computer Security Division and the Communications Security Establishment (CSE) of the Government of Canada. The use of validated cryptographic modules is required by the United States Government for all unclassified uses of cryptography. The Government of Canada also recommends the use of FIPS 140 validated cryptographic modules in unclassified applications of its departments.
Although NIST publication 197 ("FIPS 197") is the unique document that covers the AES algorithm, vendors typically approach the CMVP under FIPS 140 and ask to have several algorithms (such as 3DES or SHA1) validated at the same time. Therefore, it is rare to find cryptographic modules that are uniquely FIPS 197 validated and NIST itself does not generally take the time to list FIPS 197 validated modules separately on its public web site. Instead, FIPS 197 validation is typically just listed as an "FIPS approved: AES" notation (with a specific FIPS 197 certificate number) in the current list of FIPS 140 validated cryptographic modules.
FIPS validation is challenging to achieve both technically and fiscally. There is a standardized battery of tests as well as an element of source code review that must be passed over a period of several days. The cost to perform these tests through an approved laboratory can be significant (e.g., well over $10,000 US) and does not include the time it takes to write, test, document and prepare a module for validation. After validation, modules must be resubmitted and reevaluated if they are changed in any way.
See also
- Data Encryption Standard (DES) - a standard AES replaces
- Triple DES - a standard AES replaces
- Advanced Encryption Standard process
Notes and references
- Nicolas Courtois, Josef Pieprzyk, "Cryptanalysis of Block Ciphers with Overdefined Systems of Equations". pp267–287, ASIACRYPT 2002.
- Joan Daemen and Vincent Rijmen, "The Design of Rijndael: AES - The Advanced Encryption Standard." Springer-Verlag, 2002. ISBN 3-540-42580-2.
External links
- Literature survey on AES
- The archive of the old official AES website
- FIPS PUB 197: the official AES standard (PDF file)
- Animation of the 128-bit AES encryption process
- Very detailed AES tutorial with implementation in C
Implementations
- Current list of FIPS 197 validated cryptographic modules (hosted by NIST)
- Current list of FIPS 140 validated cryptographic modules with validated AES implementations (hosted by NIST) - Most of these involve a commercial implementation of AES algorithms. Look for "FIPS-approved algorithms" entry in the "Level / Description" column followed by "AES" and then a specific certificate number.
- A simple commented implementation in C/C++ aimed at beginners
C/ASM Library
- GPL-licensed Nettle library also includes an AES implementation
- LGPL-licensed written in C
- A byte-oriented public domain in C
- BSD licensed from Brian Gladman
- Public-domain from D.J. Bernstein
- Public domain C from Philip J. Erdelsky
C++ Library
- Crypto++ A comprehensive C++ semi-public-domain implementation of encryption and hash algorithms. FIPS validated
- Chris Lomont's public-domain version of AES
Java
- Java Cryptography Extension, integrated in the Java Runtime Environment since version 1.4.2 (see example code)
- Bouncy Castle Crypto Library
JavaScript
- Clipperz Crypto Library, includes an efficient implementation.
- Direct implementation of standard transparently coded, with counter mode of operation
- Calculator showing intermediate values
- Simple 128/192/256-bit AES with hexadecimal inputs
Other Languages
- Martin Offenwanger's GPL-licensed AES source code written in Delphi
- "Keep Your Data Secure with the New Advanced Encryption Standard" A detailed explanation with C# implementation by James D. McCaffrey.
- LGPL 128bit Implementation in PHP (Registration required)
- Rijndael Inspector Program made in Flash to encrypt/decrypt using AES-128.
File Based Encryption
- OpenSSL includes AES cipher support as of version 0.9.7 and is dual-licensed under the terms of the OpenSSL License and the original SSLeay license. FIPS validated via IBM
- Peter Selingers ccrypt file encryption utility for UNIX, GPL-licensed
- GPG, GPL-licensed, includes AES, AES-192, and AES-256 as options.
- TrueCrypt uses AES optimized in assembly language.